今回はエリンガム図の読み方第3弾として、平衡酸素分圧の読み取り方を解説したいと思います!
過去のエリンガム図の解説記事はこちらですので、是非参考にしてください!
一応、大学時代の教科書や文献で復習してから記事を作成したのですが、間違いや修正があった場合、コメント下されば助かります!
それでは解説にうつります!
とりあえず読み方だけを手っ取り早く知りたい方は、「2. エリンガム図での平衡酸素分圧の読み方」だけでOKです!
標準反応ギブズエネルギー変化(ΔrGº)と平衡酸素分圧の関係
まず、理論的な説明から入ります。
ある反応の平衡定数Kと標準反応ギブズエネルギー変化ΔrGºには次の関係があります(ここまでの導出は熱力学の教科書を見ていただきたい…)
$$RTlnK=-Δ_{r}G^{º}$$
R:気体定数
T:絶対温度
今回は金属(M)が酸素と反応して、金属酸化物(MxOy)が生成する反応を想定します。
この時の化学反応式は、
xM + y/2O2 → MxOy
ここで、酸素の前の係数を1にしておくと便利ですので式を変形します(この理由は後述します)
すると、
2x/yM + O2 → 2/yMxOy
と変形できます。
この反応の平衡定数Kはそれぞれの活量aを用いて、
$$K=\frac{a_{M_{x}O_{y}}^{2/y}}{a_{M}^{2x/y}a_{O_{2}}^{ }}$$
となります。
金属Mと金属酸化物MxOyは凝縮相(固相や液相)であるため、標準圧力近傍では$ a_{M}=1, a_{M_{x}O_{y}}=1 $と近似できます。
また、気体の場合の活量は以下になります。
$$a_{O_{2}}=\frac{P_{O_{2}}}{P^{º}}$$
・$P_{O_{2}}$:平衡酸素分圧
・$P^{º}$:標準圧力
よく文献では標準圧力に1barを使用しているので、$P^{º}=1$としていますね。
よって、平衡定数Kは
$$K=\frac{P^{º}}{P_{O_{2}}}$$
となります。化学反応式の酸素の前の係数を1にすることで、このように平衡定数を酸素分圧の簡潔な式で記述することができます。
この式を平衡定数Kと標準反応ギブズエネルギー変化ΔrGºの関係式に代入すると、
$$RTln(\frac{P^{º}}{P_{O_{2}}})=-Δ_{r}G^{º}$$
式変形して、
$$Δ_{r}G^{º}=RTln(\frac{P_{O_{2}}}{P^{º}})$$
この式から、酸素分圧がある一定の値である場合、$Rln(\frac{P_{O_{2}}}{P^{º}})$は定数となるため、$Δ_{r}G^{º}$は$T$の一次関数となるということがわかります。
エリンガム図での平衡酸素分圧の読み方
さて、いよいよ金属酸化物が生成する時の、平衡酸素分圧をエリンガム図で読み取っていきましょう。
先ほどの説明から、酸素分圧が一定の時、$Δ_{r}G^{º}$は$T$の原点を通る一次関数となるということがわかりました。
つまり、$Δ_{r}G^{º}$を$T$に対してプロットすると、直線となるということです。
金属酸化物生成の$Δ_{r}G^{º}$のグラフ上に、様々な酸素分圧における$Δ_{r}G^{º}$と$T$の関係を赤線で示した図が次になります!(この関係式は絶対温度で成立するため、直線の原点は0ケルビンの点となります)
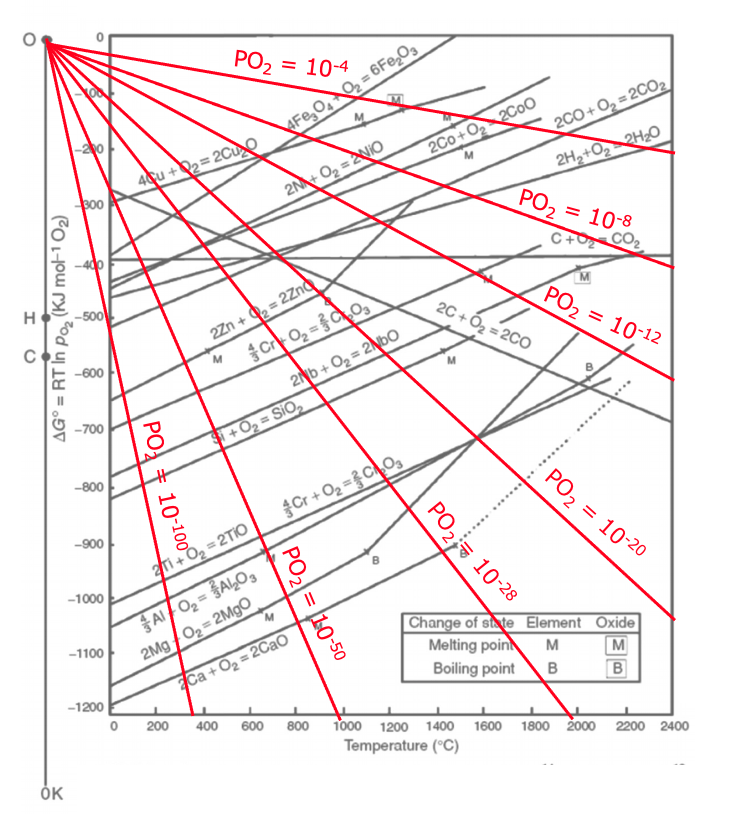
参考: Metal organic frameworks as precursors for the manufacture of advanced catalytic materials Mater. Chem. Front., 2017, 1, 1709-1745
ただ、これだとグラフがごちゃごちゃしてわかりにくいので、頭がいい人が次のようにグラフに工夫をしてくれました。
上の赤線を延長して、$P_{O_{2}}$の副尺と交わったところの$P_{O_{2}}$を読み取れば、それがその直線での平衡酸素分圧を表しています!
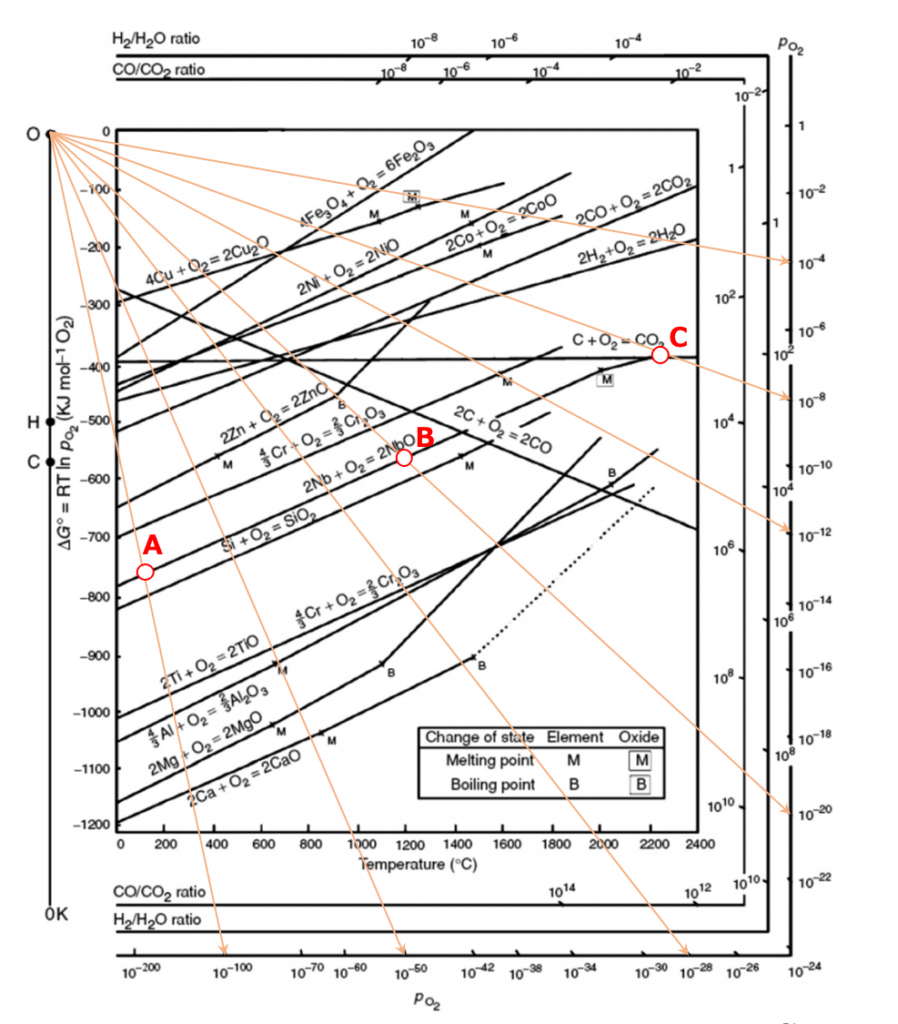
どのように使用するか例を示します。
例えば、上の図の、2Nb + O2 →2NbO
での反応における$Δ_{r}G^{º}$の直線上に私がA点、B点、C点をプロットしました。
A点は、温度100℃で$Δ_{r}G^{º}=-770kJ/mol$です。
この温度の時、平衡酸素分圧$P_{O_{2}}=10^{-100}bar$となります。
同様にB点は、温度1180℃で$Δ_{r}G^{º}=-550kJ/mol$です。
この温度の時、平衡酸素分圧$P_{O_{2}}=10^{-20}bar$となります。
同じくC点は、温度2200℃で$Δ_{r}G^{º}=-400kJ/mol$です。
この温度の時、平衡酸素分圧$P_{O_{2}}=10^{-8}bar$となります。
酸化物を加熱して高温にすると、酸化物から酸素が乖離していきますよね。
高温にすればするほど、酸化物の状態が不安定になってきます。よって酸化物として存在させ続けるためには、より強い酸素分圧中に置いてやる必要があります。
A点→B点→C点と温度を上昇させるにつれ、平衡酸素分圧が上昇しているのはそのためです。
例えばC点は、温度2200℃で平衡酸素分圧$P_{O_{2}}=10^{-8}bar$ですが、この酸素分圧よりも低い雰囲気中にNbOを置いてあげると、NbOの一部が熱分解して、Nbに還元されます。
逆に温度2200℃で平衡酸素分圧$P_{O_{2}}=10^{-8}bar$よりも強い酸素雰囲気にNbを置くと、Nbが酸化してNbOが生じるということになります。
つまり、2Nb + O2 →2NbOでの反応における$Δ_{r}G^{º}$の直線より上の領域(酸素分圧が平衡酸素分圧よりも高いことを意味)ではNbOが安定となり、直線より下の領域ではNbOはNbに分解されるということです。
また、他にも言えることがあります。
例えば2Ca + O2 →2CaOの反応は、先ほどのNbの反応よりも線がずっと下にあります。
これは高温に加熱してもCaOの方が、より低い酸素分圧で安定して存在できるということを意味しています。
(温度1180℃だと、NbOの場合は平衡酸素分圧$P_{O_{2}}=10^{-20}bar$ですが、CaOの場合は平衡酸素分圧$P_{O_{2}}=10^{-34}bar$とずっと低いですよね。)
つまり、NbとCaの混合物を温度1180℃、酸素分圧$P_{O_{2}}=10^{-34}bar$程度の雰囲気におくと、Nbは金属のままですが、Caは酸化してCaOとなります。
このように金属分離や精錬にも応用可能です。
まとめ
今回は、エリンガム図での平衡酸素分圧の読み方とその応用を解説しました!
まとめると、
・$Δ_{r}G^{º}$の直線より下の領域では酸化物は分解される
・温度と酸素分圧を制御することで、金属分離などに応用可能





