今回はエリンガム図の読み方第4弾として、平衡状態のCO/CO2分圧比とH2/H2O分圧比の読み取り方を解説したいと思います!
H2/H2O分圧比も読み方、考え方は一緒ですので、今回はCO/CO2分圧比のみを取り上げています。
この読み方が理解できれば、このようなことに応用可能です。
・金属酸化物を還元させる場合に、CO/CO2比をどの程度にする必要があるのかわかる
過去のエリンガム図の解説記事はこちらですので、是非参考にしてください!
・エリンガム図での平衡酸素分圧の読み方をわかりやすく解説します
一応、文献で復習してから記事を作成したのですが、間違いや修正があった場合、コメント下されば助かります!
それでは解説にうつります!
金属の酸化反応における標準反応ギブズエネルギー変化(ΔrGº)と平衡酸素分圧の関係
まず、金属(M)が酸素と反応して、金属酸化物(MxOy)が生成する反応を想定します。
この時の化学反応式は、
2x/yM + O2 → 2/yMxOy
と表せます。
この反応の平衡定数をK1とし、K1をそれぞれの活量aを用いて表すと、
$$K_{1}=\frac{a_{M_{x}O_{y}}^{2/y}}{a_{M}^{2x/y}a_{O_{2}}^{ }}$$
金属Mと金属酸化物MxOyは凝縮相(固相や液相)であるため、標準圧力近傍では$ a_{M}=1, a_{M_{x}O_{y}}=1 $と近似できます。
また、気体の場合の活量は次の式になります。
$$a_{O_{2}}=\frac{P_{O_{2}}}{P^{º}}$$
・$P_{O_{2}}$:平衡酸素分圧
・$P^{º}$:標準圧力
よく文献では標準圧力に1barを使用しているので、$P^{º}=1$としていますね。
よって、平衡定数K1は次の形となります。
$$K_{1}=\frac{P^{º}}{P_{O_{2}}}$$
続いて、平衡状態の時、ある反応の平衡定数Kと標準反応ギブズエネルギー変化ΔrGºには次の関係があります。
$$RTlnK=-Δ_{r}G^{º}$$
R:気体定数
T:絶対温度
今回の金属(M)が酸素と反応して金属酸化物(MxOy)が生成する反応の平衡定数K1を代入し、標準反応ギブズエネルギー変化を$Δ_{r}G^{º}_{1}$とすると、
$$RTln(\frac{P^{º}}{P_{O_{2}}})=-Δ_{r}G^{º}_{1}$$
式変形して、
$$Δ_{r}G^{º}_{1}=RTln(\frac{P_{O_{2}}}{P^{º}}) ・・・式(1)$$
となります。
$Δ_{r}G^{º}_{1}$はエリンガム図の縦軸を表しています。
この式は後で利用するので、覚えておきましょう。
COの酸化反応におけるΔrGºと各気相の分圧の関係
次に、気体の一酸化炭素(CO)が酸素と反応して、二酸化炭素(CO2)が生成する反応を想定します。
この時の化学反応式は、
2CO + O2 → 2CO2
と表せます。
この反応の平衡定数をK2とし、K2をそれぞれの活量aを用いて表すと、
$$K_{2}=\frac{a_{CO_{2}}^{2}}{a_{CO}^{2}a_{O_{2}}^{ }}$$
また、気体の場合の活量はそれぞれの分圧を用いると次式になります。
$$a_{CO}=\frac{P_{CO}}{P^{º}}$$
$$a_{CO_{2}}=\frac{P_{CO_{2}}}{P^{º}}$$
$$a_{O_{2}}=\frac{P_{O_{2}}}{P^{º}}$$
・$P$:各気相の平衡分圧
・$P^{º}$:標準圧力
これらを代入して、平衡定数K2を整理すると、
$$K_{2}=\frac{P_{CO_{2}}^{2}P^{º}}{P_{CO}^{2}P_{O_{2}^{}}}$$
となります。
続いて、COが酸素と反応してCO2が生成する反応の平衡定数K2と標準反応ギブズエネルギー変化$Δ_{r}G^{º}_{2}$を
$$RTlnK=-Δ_{r}G^{º}$$
に代入して整理すると、
$$RTln(\frac{P_{O_{2}}}{P^{º}})=Δ_{r}G^{º}_{2}+RTln(\frac{P_{CO_{2}}^{2}}{P_{CO}^{2}})$$
ここで、式(1)より
$$Δ_{r}G^{º}_{1}=RTln(\frac{P_{O_{2}}}{P^{º}})$$
であるので、
$$Δ_{r}G^{º}_{1}=Δ_{r}G^{º}_{2}+RTln(\frac{P_{CO_{2}}^{2}}{P_{CO}^{2}})$$
また、$Δ_{r}G^{º}_{2}$は温度の一次関数で近似でき、
$$Δ_{r}G^{º}_{2}=0.1698T-562.4 [kJ/mol-O2]$$
となります。
こちらの記事(エリンガム図の切片と傾きについて解説します)で説明していますが、$Δ_{r}G^{º}$の傾きの変化は、反応物もしくは生成物の状態変化(融解、蒸発等)により発生します。
COが酸素と反応してCO2が生成する反応は気体しか登場しないため、$Δ_{r}G^{º}$の傾きはほとんど一定となります。
したがって、
$$Δ_{r}G^{º}_{1}=(0.1698T-562.4)+RTln(\frac{P_{CO_{2}}^{2}}{P_{CO}^{2}})$$
$$Δ_{r}G^{º}_{1}=-562.4+T(0.1698+Rln(\frac{P_{CO_{2}}^{2}}{P_{CO}^{2}}))$$
この式から、CO分圧とCO2分圧がある一定値であるとした場合(=CO/CO2比が一定)、$Δ_{r}G^{º}_{1}$は切片-562.4kJ/mol-O2を通る温度Tの一次関数となることがわかります。
金属酸化物生成(金属へ還元)に必要とするCO/CO2比の読み方
さて続いて、金属酸化物が生成する時の(もしくは金属に還元する時の)、平衡CO/CO2分圧比をエリンガム図で読み取っていきましょう。
先ほどの説明から、CO分圧とCO2分圧がある一定値である場合、$Δ_{r}G^{º}_{1}$は切片-562.4kJ/mol-O2を通る温度Tの一次関数となるということがわかりました。
金属酸化物生成の$Δ_{r}G^{º}_{1}$のグラフ上に、複数のCO/CO2における
$$Δ_{r}G^{º}_{1}=-562.4+T(0.1698+Rln(\frac{P_{CO_{2}}^{2}}{P_{CO}^{2}}))$$
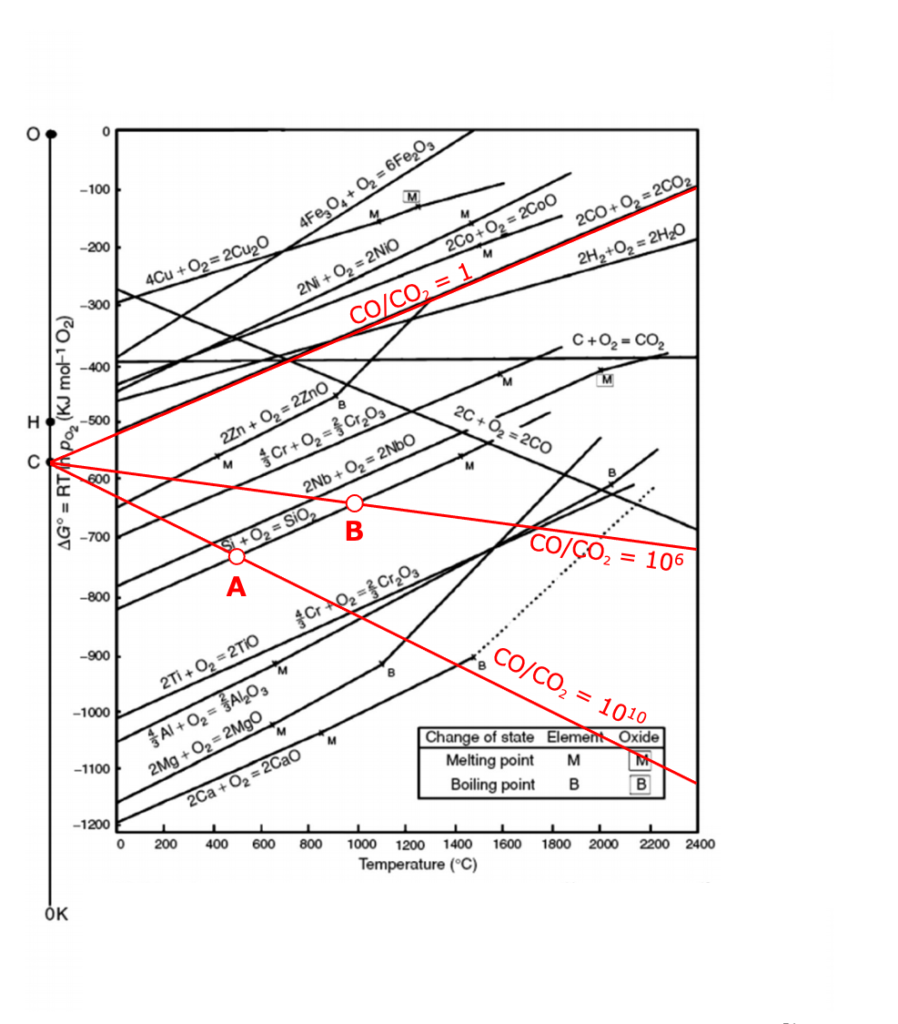
の関係を赤線で示した図が次になります。
参考: Metal organic frameworks as precursors for the manufacture of advanced catalytic materials Mater. Chem. Front., 2017, 1, 1709-1745
※資料によって使用している値が微妙に異なるため、図中の切片が-562.4kJ/mol-O2に見えないかもしれません
赤線の傾きが小さくなるにつれ、CO/CO2は大きくなり、より強い還元雰囲気となることがわかります。
Al2O3やCaOのようにエリンガム図上で下の方に位置している酸化物は、非常に強い還元雰囲気にさらされていても、すぐに酸化してしまうことがわかります。
また、当たり前ですが、CO/CO2=1の赤線がちょうど2CO+O2=2CO2の線に重なっていますね。
ただ、このグラフはごちゃごちゃしてわかりにくいので、次のグラフのように副尺と交わったところを読み取れば、より使いやすいです。
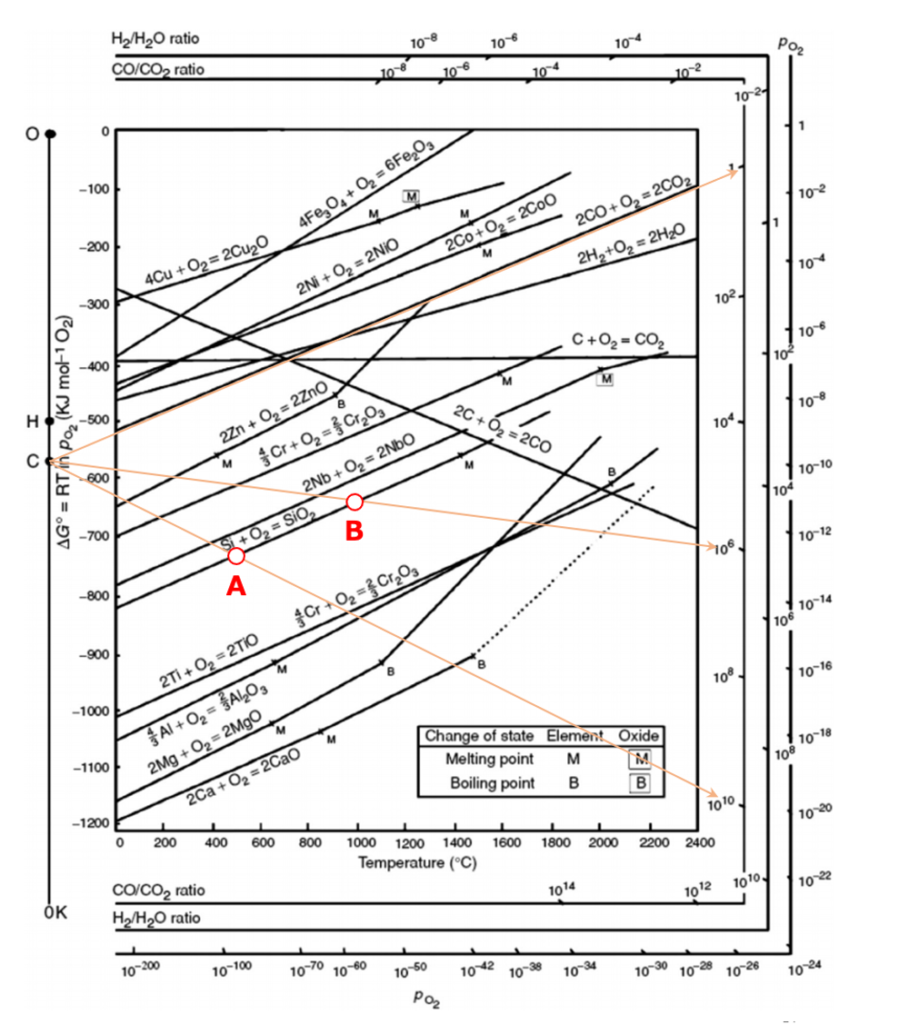
どのように使用するか例を示します。
例えば、上の図の、Si+ O2 →SiO2
の反応における直線上にA点とB点をプロットしています。
A点は、温度500℃で$CO/CO_{2}=10^{10}$です。
これは$CO/CO_{2}>10^{10}$となるような強い還元雰囲気では、金属Siが熱力学的に安定であり、$CO/CO_{2}<10^{10}$では、SiO2が安定であるということを意味しています。
つまり、$CO/CO_{2}>10^{10}$となるような強い還元雰囲気の炉に原料のSiO2を入れると、還元されてSiが生成します。
B点も同様に考えると、温度1000℃で$CO/CO_{2}=10^{6}$です。
$CO/CO_{2}>10^{6}$となるような強い還元雰囲気では、金属Siが熱力学的に安定であり、$CO/CO_{2}<10^{6}$では、SiO2が安定となります。
要は、各温度においてSi+ O2 →SiO2の直線より上の領域では、酸化物が安定となり、下の領域では金属が安定になるということです。
では例えば、温度1000℃で$CO/CO_{2}=2×10^{6}$のところ(B点より少しだけ下)に原料のSiO2を入れて、そのままの炉内雰囲気で温度500℃まで下げてみましょう。
B点で$CO/CO_{2}>10^{6}$の雰囲気では還元が進みますので、金属Siが生成します。
その後、このCO/CO2のまま温度を下げていくと(そのような制御ができるかはわかりませんが)、500℃〜1000℃のどこかの温度でSiO2の方が安定になり、500℃では完全に$CO/CO_{2}<10^{10}$となるため、SiO2が生成します。
このように、炉内の温度とCO/CO2を制御することで、金属に還元するのかどうかを判定することができます。
まとめ
今回は、エリンガム図での平衡状態のCO/CO2の読み方とその応用を解説しました!
まとめると、
・$Δ_{r}G^{º}$の直線より下の領域では還元力が強いため酸化物は分解される
・温度と酸素分圧を制御することで、金属分離などに応用可能
となります!
長文を読んでいただきありがとうございました!






