今回は絞り膨張に関して解説していきます。
私は2021年のエネルギー管理士(熱)を受験した際に、課目IIで「絞り膨張」の問題に遭遇しました。
その時は、運良く問題を解くことができたのですが、実はちゃんと理解できておらず、ずっとモヤモヤしていました。
今回、絞り膨張について勉強する機会があり、自分なりに理解することができましたので、解説していきます!
絞り膨張とは
絞り膨張とは、絞りによって気体の圧力を低下させることにより、気体が膨張する現象のことです。
また、この膨張の前後で、気体の有するエンタルピーは変化しない(等エンタルピー変化)という特徴があります。
この現象は工業的には非常に重要で、蒸気の質を改善したり、エアコンに応用されたりと様々な用途で利用されています。
今回は、そんな絞り膨張の仕組みについて解説していきます!
絞りとは
まず絞りとは、流体が流れている流路を狭くするものをいいます。
絞ることにより、流体に圧力損失を発生させ、絞った後の流体の圧力を低くさせます。
代表的な絞りはオリフィスです。
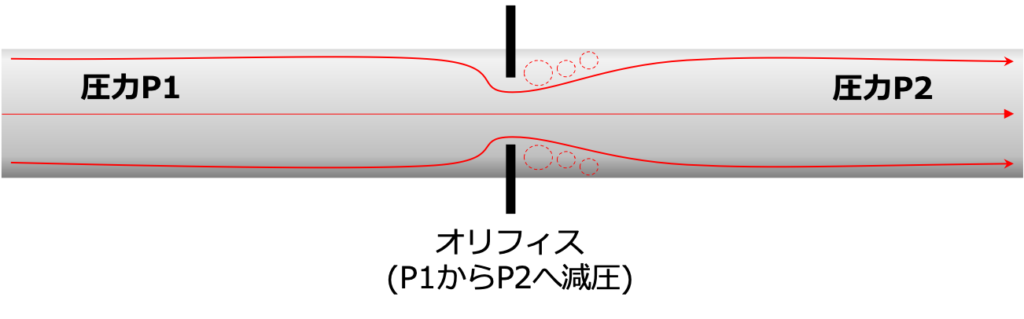
オリフィスでは、孔が開けられた板(オリフィスプレート)を配管内に挿入し、圧力損失を故意に発生させ、流体の圧力を低くさせます。
ここで最終的に流体が有する圧力P2は、初期の圧力P1よりも低くなり、圧力P2はもとの圧力P1に戻ることはありません。
また、減圧弁も絞りの一種と考えることができます。
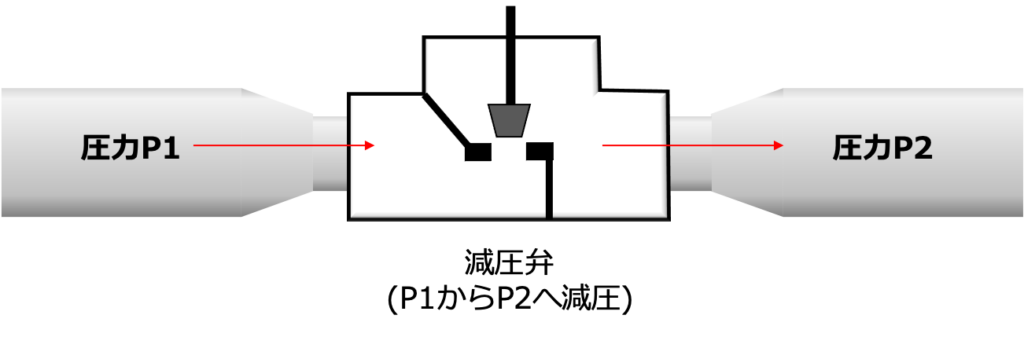
弁の開度によって流路を狭くし、流路の大きさに応じた圧力損失を発生させることで、出側の圧力を一定に保ちます。
絞り前後での気体の状態変化
次に、この絞り前後での気体の状態変化について解説していきます。
絞り前後で気体のエンタルピー(気体自体が有しているエネルギー)は変化しません。
このことを等エンタルピー変化と呼びます。
つまり、絞り前の状態を1、絞り後の状態を2とし、エンタルピーをHとすると、$$H_{1}=H_{2}$$
が成り立ちます。
こちらの記事になぜ成立するかを解説しています。
さてエンタルピーHは、内部エネルギーU、圧力P、体積Vを用いて、
$$H=U+PV$$
と表されるため、絞り前後では、
$$U_{1}+P_{1}V_{1}=U_{2}+P_{2}V_{2}$$
が成立します。
絞ったことにより、圧力P1は圧力P2に低下してしまいますので、この等式が成り立つためには、体積V2と内部エネルギーU2が変化しなければなりません。
気体の場合、圧力が下がると体積は増加するので、圧力がP1からP2に低下することにより、体積はV1からV2に増加し、内部エネルギーU2はこの等式成立のための帳尻合わせのように変化します。
この時の体積膨張を、絞り膨張と呼んでいます。
ここで、内部エネルギーU2(内部エネルギーは基本的に温度の関数)は帳尻合わせのように変化すると書きました。
気体は膨張すると温度が低下するイメージがあると思いますが、絞り膨張では、気体の種類や状態によって、マイナスの値をとる場合とプラスの値をとる場合、つまり温度が低下する場合と上昇する場合があるのです(ちなみに理想気体では温度変化しません)。
この流体の圧力変化に対して温度が変化する現象を、ジュール=トムソン効果と言います。
これは、気体が外部に仕事をすることで温度が低下する「断熱膨張」とは全く別物の現象です。
とはいえ、多くの気体ではイメージ通り絞り膨張によって温度が低下します。
珍しいですが、室温の水素は絞り膨張によって温度が上昇します。
私は当初、「絞り膨張によって圧力損失が発生したのに、なんでエンタルピーは保存されるんだろう」とちょっと引っかかっていました。
ただ、よくよく考えれば損失した圧力エネルギーは、どこかに消失してなくなったわけではなく、気体の体積膨張と内部エネルギーに変化しただけのことですね。
非圧縮性の液体の場合、絞っても膨張することはないので、圧力損失分は全て内部エネルギーに置き換えられるということですね。
(損失した圧力エネルギーが全て液体の温度上昇に使用されたとしても、上昇する温度は大したことない上、実際は配管や弁から放熱しているので、温度上昇は誤差と見なせると思います。)
まとめ
今回は、地味ですが工業的にも重要な「絞り膨張」について解説しました。
まとめると、以下となります!
・絞り膨張前後ではエンタルピーは変化しない(等エンタルピー変化)
・絞り膨張によって気体の温度が変化する現象を、ジュール=トムソン効果という
(追記)絞り膨張の応用の一例は以下の記事にまとめています。






