今回は、絞り膨張が等エンタルピー変化になる理由を解説していきます。
絞り膨張とは、絞りによって気体の圧力を低下させることにより、気体が膨張する現象のことです。
また、この膨張の前後で、気体の有するエンタルピーは変化しない(等エンタルピー変化)という特徴があります。
より詳細はこちらの記事を参考にしてください!
じゃあ、なぜ絞り膨張の前後でエンタルピーが保存されるのかを今回は解説したいと思います!
絞り前後での気体の状態変化
それでは説明していきます。

さて、断熱が施されたとある配管に細孔栓を詰めて、左側に圧力$P_{1}$、体積$V_{1}$の気体を充填しました。
細孔栓とは気体が勝手に左側から右側の領域に流れないようにするための栓です。
また、細孔栓には小さな孔が空いており、気体はこの小さな孔の流路を通過する過程で圧力損失が発生し、圧力が低下します。
それでは次に、この充填された気体を左側から$P_{1}$の圧力でゆっくり押し込んでいきます。
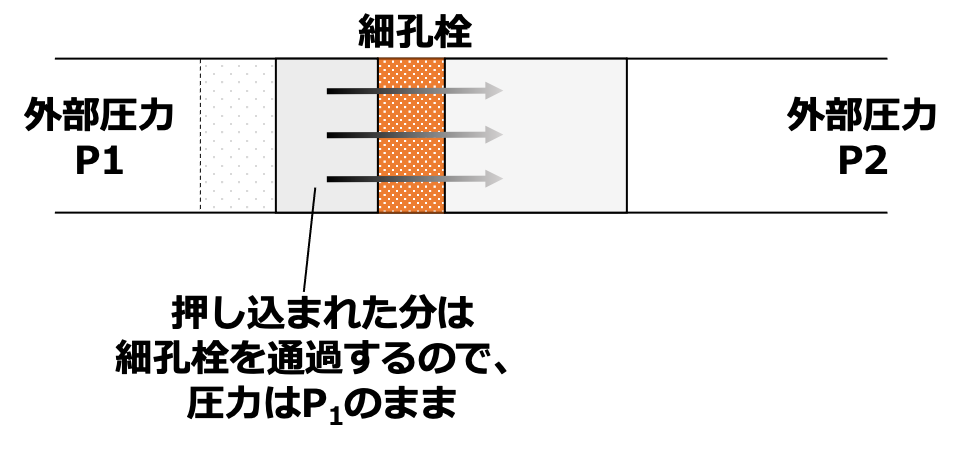
気体は細孔栓を通過するとともに圧力が低下し、圧力$P_{2}$の状態で右側の領域へと移動していきます。
最終的に、左側の気体はすべて右側に移動し、以下の状態となります。
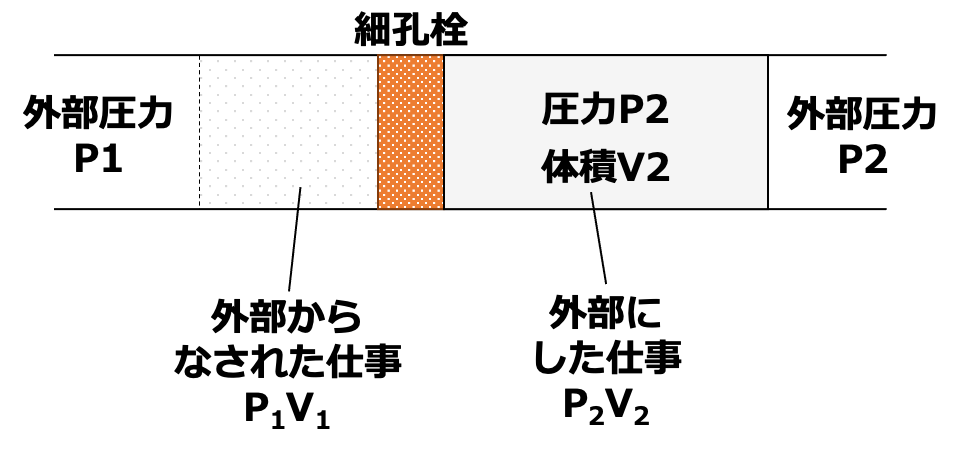
右側の気体は圧力$P_{2}$での状態で、体積が$V_{2}$まで膨張しています。
以上の工程で生じた変化を式で表したいと思います。
内部エネルギー変化$ΔU$は、系になされた仕事$W$と加えられた熱量$Q$を用いて表すと、
$ΔU=W+Q$
となります。
今は断熱されており、外部との熱のやりとりがないため、$Q=0$となります。
左側にあった気体は、圧力$P_{1}$で体積$V_{1}$からすべて右側に押し込まれました。
よって、左側の気体がなされた仕事$Win$は、
$Win=P_{1}V_{1}$
また、右側の気体は、圧力$P_{2}$で体積0から$V_{2}$まで外部に仕事をしました。
よって、右側の気体がした仕事$Wout$は、
$Wout=P_{2}V_{2}$
気体がすべて左側にある状態を1、すべて右側にある状態を2とすると、$ΔU=W+Q$で、$Q=0$であるから、
$ΔU=U2-U1=Win-Wout=P_{1}V_{1}-P_{2}V_{2}$
これを式変形すると、
$U_{1}+P_{1}V_{1}=U_{2}+P_{2}V_{2}$
$H_{1}=H_{2}$
となり、エンタルピーは保存していることがわかります。
ここまでは、細孔栓というややこしいもので検討しましたが、細孔栓の代わりに別のものを使用して、圧力損失を発生させても等エンタルピー変化となります。
例えば、オリフィスや減圧弁がそれにあたります。






